Variance vs Covariance
Variance定義:Covariance定義:
如果X=Y的話,可以看出來Var(X) = Cov(X,X)
Variance快速算法:
Covariance快速算法:
上面從第二行展開到第三行的部分:
E(XY) 就是E(XY)
E(X*E(Y)) = E(Y) * E(X),因為E(Y)這邊是一個常數
同理E(Y*E(X)) = E(X) * E(Y),因為E(X)這邊是一個常數
最後 E(E(X)*E(Y)) = E(X)*E(Y),因為本來就是常數(沒有X變數,經過E() operator之後都是常數)
這個結論倒是不用背,因為如果把Y=X,就可以直接用Var(X)得到Cov(X,Y)的式子。
Covariance / Variance of sum of RVs
covariance其實是計算一堆(不一定是independent)random variables的和的variance中間的某個產物,稱為covariance:還是有必要一行行看清楚上式:
第一行是variance的定義無誤,
第二行E( (SUM_i=1_to_n(Xi))^2)
= E( (X1 + X2 + ... + Xn)^2 ) = E( X1^2 + X2^2 + ... + Xn^2 + X1X2 + X1X3 + .... )
= E( X1*(X1 + X2 + .. + Xn) + X2*(X1 + X2 + ... + Xn) + ... + Xn*(X1 + X2 + ... + Xn) )
= E( SUM_i=1_to_n(Xi * SUM_j=1_to_n(Xj) ) /*把 j項目當作常數分離出來 */
= E( SUM_i=1_to_n(Xi) * SUM_j=1_to_n(Xj) )
這邊弄懂上面就懂了
所以簡單來說:
舉例來說:
注意:
(1) 右邊左上到右下的對角線的terms,其實就是Var(X1) + Var(X2) + Var(X3)
(2) Cov(Xi,Xj) = Cov(Xj, Xi),這個根據定義不證自明
所以右邊“矩陣”我們可以從以上兩點性質歸納出(以下兩種可能的重寫):


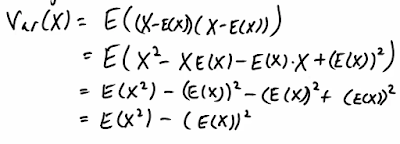






沒有留言:
張貼留言