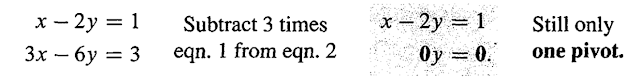upper triangle
簡單來說就是要把system of linear equations變成一個upper triangle:或是:
有時候可以重新排列一下equations的順序,方便elimination:
Pivots
原本的system中的每個equation的第一個element都是pivot,負責把下面rows同樣column位置的element消除掉。最後形成的upper triangle的對角線位置剛好就是這些pivots。Singular: 無解的狀況
事實上這是一組平行線,當然無解(交點)了:
Singular: 無限多解
elimination到最後,發現其實變成n個式子但是有 > n 個 variables:Singularity
上面兩種非唯一解稱為(singular),意思是只有一個pivot可以做elimination,而有唯一解的system不會只有一個pivots。3個unknowns equations的狀況
system:1st pivot是第一row的 2x,用它來消去row 2的 4x和 row3的 -2x,新的row2和 row3形成:
再來row2的1y 是2nd pivot(可以看到這是一個recursive process),用來消除row 3的 1y:
所以我們透過消除法把原本Ax=b 變成 Ux=c,這邊U = upper triangle:
這個Ax = b 轉變成 Ux = c的過程,稱為forward elimination,U中的對角線就是所謂的pivots,pivots經過elimination才會正確找出來。
upper triangle的好處是,其中一個變數立即有解,然後通過back substitute一一解出其他的變數。
Elimination matrix
Ax=b在做elimination的過程中,b事實上也是同步在做加減乘除。事實上這相當於vector b乘上某一個matrix E,或是說一個elimination matrix E 施作在 vector b上:由於b中的每一個element都是E的row 和 b的dot product,所以有時候光看E的row大概就能知道b會被 E "施作“ 成什麼樣:
如果E是identity matrix I,則可以看到b的element與I的row dot product就是那個component自己,或直接說 I * b = b:
如果elimination matrix 是以下這個:
則我們可以知道對b3來說,它減去了b1 * (4),這個elimination matrix成就了新的b3,在原本的forward elimination過程中,這E代表了要形成upper triangle過程中,透過pivot 1把row 3的第一個element消除成零的過程。