模型用處
通常用來model “等待某個長度時間”的機率,例如下一次部車子經過的需要再等待15分鐘的機率。fx(X)
density的圖形長這樣:CDF
由complement P(X>a):去找CDF = P(X<=a)最簡單:
CDF圖形長這樣:
E(X) & SD
這個之前都證過了(要用到u-substitution & L'Hospital's rule)Var(X)
先算E(X^2):
Memoryless
這個model是唯一continuous RV有memoryless的性質,可以將conditional probability轉化成unconditional probability:上面的語意為“如果已經等了超過八分鐘,那我們還需要再等14分鐘以上的機率,相當於需要等超過六分鐘以上的機率”。
P(X>a) = 1 - CDF(a)
如果按照conditional probability的定義去算,可以證明以上memoryless性質:
可以generalized成:
Minimum Problem
不知道為什麼,老師一直把minimum單獨拿出來講?假設有兩個independent exponential RV X和Y,令Z = min(X,Y),問E(Z)?
思考邏輯是(1)先找CDF(Z) (2) 微分求出density (3) 積分找出expectation of Z
(1) 這邊找CDF又用了先找complement P(Z>a)的方法,可能是因為independent RV可以快速求出probability:
不過特別的是,這是一個exponential RV! 由上式可以看出這是一個lambda = lambda1 + lambda2的exponential RV。
density為:
既然我們有了他的lambda,其實就套用一般exponenetial RV的公式很快就能求解:
E(Z):
不過以上的特殊行只成立在
(1) X Y independent
(2) Z = min(X,Y)
如果Z= max(X,Y),Z並不會是一個exponential RV! 要注意!
這個特性可以擴展到n個independent RVs:






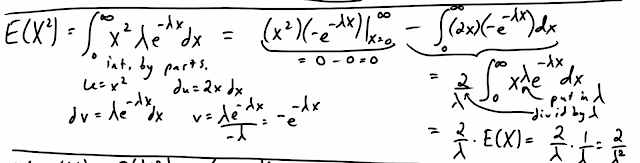





沒有留言:
張貼留言