定義
如果已知某個event B發生的機率大於0，則如果B確實發生了，A發生的機率為：
換句話說，A發生的機率可能會受到B是否發生了而改變！
直覺解讀1: 可以看成event B為新的sample space，所以A交集B的event才符合B發生前提之下，A也發生的event
直覺解讀2: 轉換成以下等式：
Independence和conditional prob.
別搞混了！A和B是獨立事件的定義為：
而P(A|B)的定義為：
所以可以看到當A和B為independent時，P(A) = P(A|B)，反向亦成立，這是iff關係。直覺上解讀就是即便我們知道B確切發生了，但這不改變我們對P(A)的看法，則A和B為獨立事件。
Conditional Probability就是一般的機率，遵守機率三公理
標題的陳述是可以證明出來的，所以當把B視為一個新的sample space（因為已知B確切發生了），P(A|B)遵守機率三公理：
一個範例
把B當成新的sample space計算會很快，也比符合直覺，不過不管怎樣，總是能回歸定義去計算：
可以看到P(A|B)和P(B|A)並不對稱，事實上這也是符合預期的。
MIT課程補充：雷達範例
conditional probability適合用來一直改進我們對某件事情的認知(probabilisitic model），舉以下例子。令event A = 真的有飛機飛過
event B = 雷達偵測到物件
以下的probability tree說明了conditional probability扮演的角色：
這邊也再次提到令人震驚的條件機率：P(真的有飛機 | 雷達偵測到物件)
這不知道對決策是好是壞的影響？
generalize conditional probability to multiplication rule
如果是牽涉到三個event:
最general form:
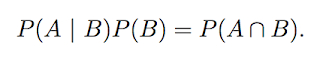
沒有留言:
張貼留言