Statistics筆記15 - Binomial Distribution

由於Purdue Probability已經教過過很多Binomial distribution的知識，這邊都是重複的，就不記錄了。

用R算binomial distribution

dbinom接受三個參數，第一個是成功的次數，第二個是全部trial的次數，第三個是成功的機率：

解讀Binomial Distribution

以下的題目我們簡單算出mean和SD:

mean = 13，意思是在一百個人裡面random sampling的話，平均會有13個人是engaged at work，因為expected value本來就每個outcome被機率權重的觀念。

所以每次sampling都是一個圍繞這mean的數字，這個圍繞的變動程度就是看SD，“平均”（因為SD也是跟mean相關的statistics）來說，3.36人次的標準差變動程度，也就是通常(99.7%) 會在2個標準差內的sampling結果會出現。

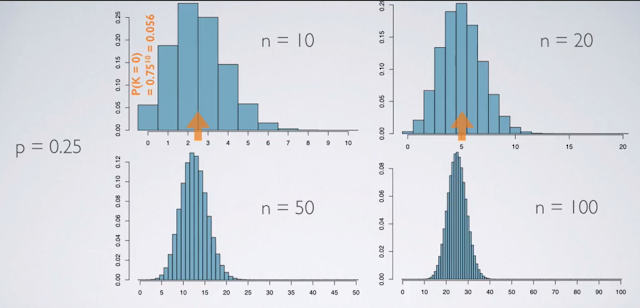
n越大，binomial distribution會趨近normal distribution

（這應該是純粹計算出來的，因為不需要做實驗）。如果把成功次數放在x軸，其相對機率放在y軸，則會發現當n大的時候，整個probability distribution的形狀會很像一個normal distirbution：

這個提供了快速解binomial probability的方法。


但是如果我們無法plot成以上的圖形，一個基本的判斷binomial distribution是否nearly normal的方法是（以下兩者皆必須成立）
E[X] = np >= 10        /* expected successful times */
E[Y] = n(1-p) >= 10  /* expected failure times */

符合以上兩個條件的話，我們可以安心用normal distribution來approximate binomial。

Facebook範例

題目如下：

這一題乍看之下看不出來是binomial distribution。
白話文就是一個人平均有245個FB朋友，而且我們知道FB上有25%的人是power users。

所以245個朋友中，任意一個是power user的機率p = 0.25，不是的機率q = 0.75
讓random variable K為power user朋友的數目，問P(K>=70)?

這樣解讀就是一個標準的binomial distribution problem。

之前Purdue機率課的算法如下：

P(K=70) = choose(245,70)*((0.25)^70)*((0.75)^(245-70))
P(K=71) = ...
.
.

突然腦子當機，好像不知道怎麼算，目前似乎沒學過要怎麼算binomial probability X >= x的方法。


那就用normal distribution來逼近吧：
這個binomial distribution的“形狀”像是normal，所以其mean就是normal的mean，其SD就是此normal的SD：

我們等於要找出P(X>=70)，可以算出Z-score用查表法，或是直接用R的
1- pnorm(70, 61.25,6.78) = 0.09842807

可是如果我們真的把算出P(X>=70)，答案如下：

有點差距！原因在於我們用continuous distribution來model discrete data，至少就少了P(X=70)這個機率，因為在continuous probability中，單點機率為零。

這就讓我想起機率課中說的continuity correction!

不過比較奇怪的是，在這邊統計課是把P(X>=70)換成P(X >= 69.5)，而不是P(X >= 70.5)，這是沒錯的，畫出數線來看就知道了，因為binomial distribution是discrete RV，所以X只能是整數：

  68     69  |    70       71
(no) (no)    (yes)  (yes)

continuity correction是取no和yes的整數交界的中間值，所以是69.5。

這樣就跟用R直接算出sum of binomials幾乎一樣了。

範例2

這是一個binomial probability problem。
#trials n = 10
P(success)  = 0.56
令X為成功的次數，求P(X = 6)?

機率方向的思考：

P(X = 6) = choose(10,6) * 0.56^6 * (1-0.56)^4

用R驗證也沒錯：

統計方向的思考：
跟機率思考方向一樣啦！！！！
因為這個已經有明確的binomial distribution參數了，不需要用normal distribution去逼近。何況n還不夠大！

不去計算的話，常理推斷10個裡面出現“剛好”6次成功，當然機率遠比1000次裡面“剛好”出現600次成功藥膏太多了。

答案是b

這一題是在問，這個binomial distribution是否是nearly normal?

我們上面已經有兩個必須檢驗的條件：

E[X] = np >= 10        /* expected successful times */
E[Y] = n(1-p) >= 10  /* expected failure times */

的確是沒錯！

最後：

這跟FB範例那一題一樣，我們要求P(X=60) + P(X=61) + ... + P(X=100)，手動計算會死人，但是基於上一題中我們已經驗證此binomial distribution是一個nearly normal distribution N~(mean = 56, SD = 4.96)，我們相當於是要在此normal distribution中找出P(X>=60)

但是要加上continuity correction，因為我們用continuous distribution去approximate discrete distribution：

59  |   60
(N)     (Y)

取59.5

正確算法當然要轉成Z然後查表，不過既然已經有了R，就直接算吧：