Data即便看起來不像是直線,也可以apply linear regression
例如下面這個data set:明顯的,我們找不出一條直線方程式可以適合的fit這個data set,但是我們可以找出一個x的三次方程式,配上一個係數vector w:
我們此時可以用linear regression來找出w,為什麼?
1-D Polynomial Regression
因為linear regression的定義是:prediction f和未知數w是線性關係(不會出現w的次方>=2),跟x無關:所以即便用一個x的三次方程式來fit data set,只要w的次方<=1,就是一個f的linear function。
所以對一個polynomial x function才能fit data set的problem來說,我們可以把所有的input data寫成一個matrix X (最高次方p),當然要記得加上x0項 = 1:
接下來就是解optimize least squared error,答案仍然是一樣的:
Underfitting & Overfitting
如果用x的0次方程式來fit某個1-D data set如下:由於我們只需要找到w0,所以根本不用管xi data,所以X matrix只會有一個column,而且全部都是1。最後找到的least square polynomial只是一個常數函數 f = w0,見上圖。這是underfitting。
如果用x的一次函數來fit這個data set的話,仍然是underfitting:
如果用x的三次方程式來fit這個data set的話,看起來是最好的:
提醒一下,預測出來的y' = w0 + w1*x1 + w2*x2^2 + w3*x3^3
如果我們自作主張,用x的十次方函數來fit這個只有十個點的data set:
可以看到最後形成的least square prediction f即便可以通過所有的點(因為有十個點對應十個未知數w0 ~ w9,一定能解出這十個連立方程式),但是完全不具預測性。這就是overfitting。
2-D以上Polynomial Regression
以下slide講得很清楚,懶得打字啦:Summary
polynomial regression基本上就是linear regression的x function高次方版本,可以寫成通式如下:不論g(x)是什麼,只要f和w的關西是線性的(w次方 <= 1),則我們都可以使用least square estimation來找出w vector,做出一個prediction function y' (or say f):




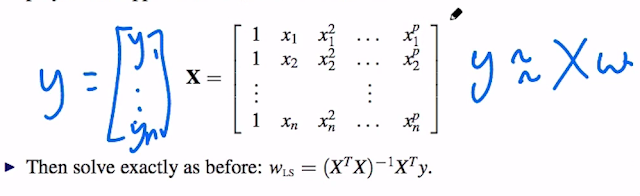







沒有留言:
張貼留言