AI筆記20 - Linear regression models

Supervised Learning

regression和classification都是supervised learning的一種。
regression是找出一個function f (稱為regressor)，然後將input d-dimensional vector map到某一個實數：

而classification是將找出一個function f (稱為classifier)，map input vector到某幾個categories:

Linear Regression

有一些label好的data yi：

我們要learn 一個function f來 best fit這些data。
為什麼稱作linear regression? 因為此function f可以用一個線性方程式表示。舉例來說，一個1-d vector，可以在2-d平面上找出一條直線方程式：

當然我們知道此直線方程式有y=ax+b的型態，用這邊的符號寫成：

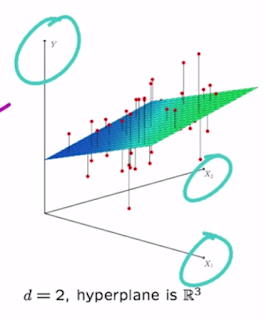
同樣的如果data是2-d vectors，我們再加上y value組成的3-d空間中可以找出一個hyperplane best fit：

當然此平面方程式如下：

我們可以歸納出通式，而實際上所謂的learning linear regression model，是在找出optimal 係數（係數扮演著每一個vector element的權重）：

要找出最適當的係數的話，可以使用least squares當作loss function，平方意義是不用擔心負值：

圖示的話如下，我們要對所有的loss的和做minimization:

我們定義要minimize的function稱為risk或是cost function，下面是一個平均loss的cost function，多乘一個1/2係數是之後微分可以cancel掉：

Linear Regression Learning範例

如果有一個1-d vector labeled dataset，我們知道其linear regression function會是以下的形式：

loss function採用least squares的話，則cost function或說risk如下：

如果把f(x)的定義帶入上式，則R變成一個beta的function，因為我們要求的是最適當的beta，所以beta變成了變數了：

注意雖然f是linear function，但是cost function是一個二元二次方程式，在空間中是一個bowl:

可以看到讓risk最小的(beta0, beta1)處於bowl正中心，所以有一個global minimum。

找出能minimize risk的beta，數學上可以寫成以下：

根據微積分，找出最小值就是偏微分各變數，並在等於零的時候算出：

Normal equations

我們可以把Risk function R寫成matrix form：

則R可以重寫成：

做偏微分：

做二次微分判斷有無極小值：

極小值只發生在二次導數為零時：

所以我們可以直接從learning dataset X算出optimal beta! 

不過當(X^T)X沒有inverse時，就無法算出來。另外用演算法去找此inverse在vector dimension很大的時候，會是O(d^3)！

Gradient Descent

如果(X^T)X沒有inverse的話，另一個找出optimal minimum使得risk最小化的方式是gradient descent，這算是一個持續不斷直到收斂的過程：

R function的一次微分就是gradient function，在一個變數時稱為斜率，這也就是gradient descent的由來，我們要找出R gradient為零的時候的beta值，演算法如下：

可以看到我們必須同時update/descent 所有的beta，這樣才能在空間中同時個變量都往minimum前進，所以可以看到beta - alpha * 斜率，alpha稱為“learning grade”，用來控制descent的速度。

對1-D feature vector來說，我們之前已經算出beta0和beta1的偏微分：

所以演算法可以寫成：

Implementation忠告

第五點跟線性代數有關....之後再來補充為什麼？！