alpha-beta Pruning
ab pruning是找出某些不需要search的subtree。舉例來說,以下是一個minimax search tree :
假設只搜尋到深度2就必須要做決定,則root Max最後的utitlity score為3。
現在問題是,有必要explore這麼多node嗎?答案是不一定!
舉例來說,如果以下X Y是尚未explore的nodes:
我們知道root Max要做決定的話,要取max(3, Z, 2)
但是由於Z = min(2,X,Y) <= 2 < 3,所以我們不care Z多少了,因為對我們要取max來說沒貢獻了。
所以不必explore X Y就可以知道 root Max要取 max(3 , DONT_CARE, 2) = 3
這樣馬上就省略了一個subtree需要去explore!
演算法
alpha-beta pruning仍然是一個minimax演算法(DFS),但是添加了pruning的機制。我們需要多兩個輔助變數:
alpha - 目前Max可做的move的最大utility score ,所以初始化要是 -INF,只能被Max node update
beta - 目前Min可做的move的最小utility score,所以初始化要是 +INF,只能被Min node update
當 alpha >= beta 的時候,我們就有pruning發生了!!! 為什麼?
對一個min node來說,它看到目前的parent max node的alpha/beta值,而這個min node只能藉由其children的utility score來update beta值。如果它發現alpha >= beta,由於此min node能回傳的utility score最大也只能是目前的beta,意即此min node再也無法提供其parent max node大於目前alpha值的utility score,所以剩下的所unexplored的children都可以prune掉不看了。
同理,對一個max node來說,它看到目前的parent min node的alpha/beta值,而這個max node只能藉由其children的utility score來update alpha值。如果它發現beta <= alpha,由於此max node能回傳的utility score最小也只能是目前的alpha,意即此max node再也無法提供其parent min node小於目前beta值的utility score,所以剩下的所unexplored的children都可以prune掉不看了。
範例
1. 首先alpha, beta被initialized at root Max,然後root Max開始explore所有的children,先選 child B:2. Min node B 也explore自己的children,並且根據回傳的utility score來update beta = 3:
3. 此時對root Max來說,第一個action child node已經explored,回傳utility score給root Max:
4. root Max node此時要根據回傳的utility score update alpha,的確是需要update,因為3 > alpha = -INF:
5. 再來root Max A 繼續explore C:
6. Min node C 也往下explore自己的children,首先update了beta = 2:
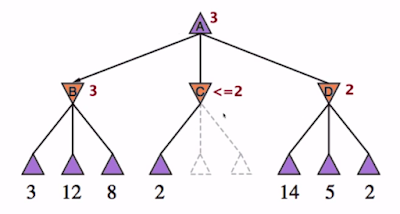
7. 這邊發生了Pruning!
因為 min node C 發現了目前(alpha = 3) >= (beta = 2),這表示Min node C最大的utility score只能是2(因為C只能從children中選擇 <= 2的utility score),而對root Max A來說,既然child C最大只能回傳utility = 2,但是目前已經有找到一個utility score = 3 = alpha了,那C這個node是不會被 root Max A所選擇的,所以剩下的C的unexplored children也不會造成任何影響了,可以放心的prune掉。
8. A 繼續explored child D:
9. Min node D也完成utility score的計算,最後update beta = 2:
10. root Max A完成了所有的child node的utility score計算,最後得到自己的utility score = max(3, 2, 2) = 3
真正tree expansion的過程如下:
最後結果:
Ordering & Performance
explore children nodes的順序會影響pruning的結果,例如上圖中如果node D先explore value = 2的leaf,則剩下的nodes(14 5)都不用在explore了。如果pruning完全沒發生,則complexity = minimax search = O(b^m),m是DFS最深的depth。
如果大量的pruning發生的話,(應該是平均來說)complexity可以降到O(b^(m/2)),亦即平均可以比minimax多搜尋一倍的深度。
怎麼達到一個好的ordering? 可能有以下方法(沒很詳細說明):
Heuristics
即便使用pruning技巧,minimax search還是得要抵達leaf node才有辦法獲得utility score,真實世界的比賽不可能每一步都給你這麼多的時間思考。所以一種可能提早獲得決定的方法就是捨棄使用end state leaf node的utility score,而是對intermediate state採用evaluation function,換句話說就是使用heuristics。heuristics牽扯到domain knowledge,當然最好就是能跟utility score一樣的相對大小(理想上)。
evaluation function通常牽涉大量的feature fi與model param wi,這可能需要ML的技術來找到最好的model params:





















沒有留言:
張貼留言