Linear Regression
之前的ML/AI筆記已經詳細寫過相關的東西,這邊就不用再寫了。
LR假設了一個線性的結構,所以無法調整model complexity,永遠是一條直線(對此1-feature dataset來說),但是 KNN並未對dataset和feature間的關係設下任何假設,所以是可以調整model complexity藉由調整k值的話。
在此dataset中,剛好LR適合因為假設正確,所以有較高的R^2 score在test set上。
Ridge Regression (Linear Regression with Regularization)
Ridge regression的cost function 多了一個紅色框起來的term:
由於cost function是要做minimization才能得到我們要的w和b係數,所以加上一個跟w係數有關的term就是要penalize較大的w係數 (稱為L2 penalty),為什麼?
較大的w係數和可能導致高的model complexity,也就是會overfitting,所以regularization可以避免overfitting的問題,獲得較好的generalization model。(feature dimension高才會有影響)
alpha值就是這個penalty的強度,所以如果不要regularization,就把alpha設成零就好。
alpha越大,則optimization的結果會prefer w係數更小的model。
regularization也是跟test performance呈現此類分布,通常中間值的alpha會得到較好的test set R^2 score:
regularization對dataset小且feature數量高的dataset是較有影響,其影響性隨著dataset變大而減少。
不過用同一個dataset,為何ridge regression的R^2 score會遠比ordinary linear regression差呢?
對付這種問題就要對data做preprocessing,特別是feature normalization,把所有的feature 都放在同一個 scale上,例如都normalized成 0 ~ 1之間,以下是常用的minmax normalization:
另外training scaler和test scaler要同一個尺度(前一段已經enforce這一點),否則可能會造成random data skew,所以可以看到以下的code我們使用了同一個scaler在兩個data set上:
當然經過normalization過的data人類解讀上就會有點困難了,例如房價變成0~1之間,很難理解。
使用了normalization之後的ridge regression,在兩個test set拿到了較好的R^2 score:
Linear regression
Ridge regression without normalization
Ridge regression with normalization
不過這其實是會達成automatic feature selection,因為最小的|wj|只能是0,所以在minization過程中,最好的答案會是選擇|wj|的和為最小者,也就是跟model無關的feature會自動被剃除,或是其係數非常接近0。
可以看到用同一個dataset,Lasso regression給出的係數陣列多數是零:
也由於L1 penalty這個feature selection特性,所以Lasso regression適合用在可能少數features決定prediction model的情況中,否則應該ridge regression才比較適合:
不過要小心這樣的transformation會overfit dataset,所以必須要伴隨regularization。
可以看到不只polynomial regression比linear regression / ridge regression 在這個crime dataset有較高的R^2 score,加上regularization的polynomial regression還有更好的R^2 score on test set:
由於cost function是要做minimization才能得到我們要的w和b係數,所以加上一個跟w係數有關的term就是要penalize較大的w係數 (稱為L2 penalty),為什麼?
較大的w係數和可能導致高的model complexity,也就是會overfitting,所以regularization可以避免overfitting的問題,獲得較好的generalization model。(feature dimension高才會有影響)
alpha值就是這個penalty的強度,所以如果不要regularization,就把alpha設成零就好。
alpha越大,則optimization的結果會prefer w係數更小的model。
regularization也是跟test performance呈現此類分布,通常中間值的alpha會得到較好的test set R^2 score:
regularization對dataset小且feature數量高的dataset是較有影響,其影響性隨著dataset變大而減少。
不過用同一個dataset,為何ridge regression的R^2 score會遠比ordinary linear regression差呢?
Feature Preprocessing and Normalization
regularization的目的就是避免最後optimization結果找出的是w 係數和過大者,w係數和過大者有可能是全部都很大,或是其中幾個係數特別大,如果是後者的話,也就代表features之間的度量尺度差距太大。所以此時提高alpha值,只會對某些feature在optimization的結果造成影響,不是公平廣泛性的regularization ,因為各個feature在被prefer盡量小的過程中,contribution是不一樣的,換句話說對penalty的貢獻是不平均的。對付這種問題就要對data做preprocessing,特別是feature normalization,把所有的feature 都放在同一個 scale上,例如都normalized成 0 ~ 1之間,以下是常用的minmax normalization:
使用sklearn.preprocessing 的MinMaxScaler
有一點必須注意就是一定要用scaler在training set,不可用在test set,否則會造成data leakage! 也就是說在training過程中,不能洩漏任何test set 的資訊,否則training結果是有可信度問題的。另外training scaler和test scaler要同一個尺度(前一段已經enforce這一點),否則可能會造成random data skew,所以可以看到以下的code我們使用了同一個scaler在兩個data set上:
當然經過normalization過的data人類解讀上就會有點困難了,例如房價變成0~1之間,很難理解。
使用了normalization之後的ridge regression,在兩個test set拿到了較好的R^2 score:
Linear regression
R-squared score (training): 0.668 R-squared score (test): 0.520
Ridge regression without normalization
R-squared score (training): 0.671 R-squared score (test): 0.494
Ridge regression with normalization
R-squared score (training): 0.615 R-squared score (test): 0.599
Lasso Regression
這跟Ridge regression幾乎一樣,只是penalty function採用了sum of absolute w係數,稱為L1 penalty:不過這其實是會達成automatic feature selection,因為最小的|wj|只能是0,所以在minization過程中,最好的答案會是選擇|wj|的和為最小者,也就是跟model無關的feature會自動被剃除,或是其係數非常接近0。
可以看到用同一個dataset,Lasso regression給出的係數陣列多數是零:
也由於L1 penalty這個feature selection特性,所以Lasso regression適合用在可能少數features決定prediction model的情況中,否則應該ridge regression才比較適合:
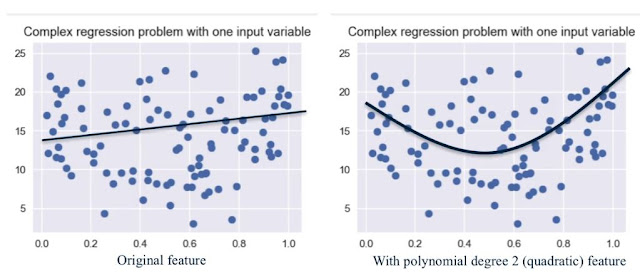
Polynomial Feature Transformation
如果feature太少,但是dataset看起來就不是linear separable,此時可以增加feature維度,來捕捉原本features之間可能的相關性。不過要小心這樣的transformation會overfit dataset,所以必須要伴隨regularization。
可以看到不只polynomial regression比linear regression / ridge regression 在這個crime dataset有較高的R^2 score,加上regularization的polynomial regression還有更好的R^2 score on test set:










沒有留言:
張貼留言