Generating model
NBC是generating model系列方法的一種。至於什麼是generating model...不知道 not yet。Bayes Theorem
根據貝式定理:
這個之前都講過了。
把這些probability給一些名詞定性吧:
也就是P(A)為還沒觀察到B之前普遍的A事件發生機率，而P(B)則為某可觀察事件之發生機率，一旦觀察到B發生了，我們會利用條件機率來改變我們對A事件發生地相信機率，也就是P(A|B)，稱為posterior。
最後P(B|A)比較特別，稱為likelihood，這反過來觀察如果A發生了，B發生的機率。\
Marginal Probability
這個probability課程都講過，基本基本的。
所以P(B) = P(A and B) + P(~A and B)，同理可以算出P(~B)。
Bayer rule可以利用marginal probability擴展成新的形式:
簡單的病理測量例子...又來了
似乎講到bayes rule都會舉這個例子，好吧，複製貼上就好:
Bayes Classification
利用機率來做classification，我們最終是要得到一個prediction function:
但是是透過conditional probability的形式:
這邊有兩種approach可以來model P(y|x)。
1. discrimitive algoritms:這就是找出decision boundary的演算法，算是直接model p(y|x)，要預測時就看怎麼算出一個sample該落入的區域。
2. generative algorithms: 這個就是用到bayes rule，事實上是建立兩個models:
最終利用此上面兩個probability以及bayes rule算出p(y|x):
在做prediction時，要找出某個y使得p(y|x)最大，此y就是其分類。不過計算上似乎可以用逼近的方式，至於怎麼導出來的....沒講!
Bayes classifier計算非常簡單，而且假設過於天真(名稱由來，但若沒有天真假設，則很難實現，後面會講)，但是實務上卻是有運行效果(happens to work! 老師講的...奇怪的形容詞)。例如做在spam detection，效果可以與decision tree / neural networks 相比。
Naive Bayes classifier settings
基本上還是一樣的classification problem setting:
假設現在有一個新的sample 需要做prediction:
代入naive bayes classifier:
這邊的問題在於怎麼從training data來model p(y)和p(x|y) ?
p(y)好model，如果training dataset夠大的話，用y出現的頻率來model是合理的。
但是p(x|y) = p (a1,a2,....ad |y) ，這個除非真的每個特定x的發生頻率高，否則model不了這個probability。怎辦? 這就是為什麼說天真的原因，因為我們要假設features之間是conditionally independent..........
我們可以把這個近似方法帶入上面的Bayes classifier重寫如下:
演算法
其實演算法就是上面那條公式而已，找出p(y), p(aj|y)，全部都是靠training data中的統計出現頻率而已。沒有一個真的"model" (e.g. function)。
範例
假設一個dataset:
由於計算很簡單，直接貼上算式:
所以是建議雇用............
雖然也是低低的probability。
根據dataset不同，有時候會發生趨近於零的probability，由於某些conditional probability of some features approaches to zero。有個調教的方法。
M-estimate
簡單來說就是在用頻率估算conditional probability的時候，同時在分子分母加上非零的"假的sample數目"。
分子的假的sample數目 = m*p，p是prior believe，也就是這個feature出現的機率，如果未知的話就用uniform distribution，也就是如果有k種feature，則此feature出現機率為 p= 1/k。
這完全是人訂的，沒有絕對就是。
例如在text classification採用Bayes classifier的時候，m-estimate可能如下:
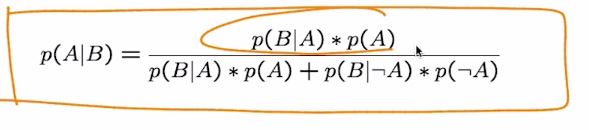
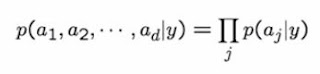
沒有留言:
張貼留言