Exploit graph structure
如果把constraint graph研究一下,能找出幾個connected components的話,那就會大大降低search complexity。下圖中T(tasmania)和澳洲大陸是分開的,所以對於coloring map這個problem來說,其實可以變成兩個subproblems:如果有n個variables和d個domain values,在BTS中 d為branching factor,而n就是整個tree的最大高度。所以整個search的running time complexity = O(d^n),如果能拆成c個subproblems的話,branching factor一樣,但是n會變小成 n/c,所以整體上就是O((c/n)*d^c),減低了非常多!!
如果有n=80個地圖要上色,僅管只有兩個顏色,d=2,但整個tree的nodes仍然需要2^80個! 如果如果能拆成4個subproblems的話,那就只有4 * 2^20個nodes。兩者相差了2^60倍! 計算時間差距約為400萬年。@@
可惜的是,要切成subproblem可說是機會很低的。
Exploit Tree structure with Directed Arc Consistency (DAC)
一個CSP可以叫做DAC,如果variable X1, X2, ... Xn是形成tree structure(相對於雙向constraint的graph),所以兩個node之間只有一個edge連接。要assign variable就任意選一個variable當作這個tree的root,先做一次topological sort,這是要讓之後做arc consistency能在linear time解決。topological sort就是根據tree中的parent/children order (因為只有單向edge)來sort:
根據wikipedia: On a graph of n vertices and m edges, using a serial computation, the algorithm above takes Θ(n + m) time; i.e., it is linear.
再來就是對這個sort好的tree做arc consistency,這需要O(n-1),因為已經sort好了。
再來每條arc consistency需要O(d^2)時間,因為arc兩端的nodes中所有的domain value pairs都要檢查。所以總共的running time complexity為:



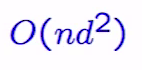


沒有留言:
張貼留言