Scala Parallel Programming筆記 6 - Parallel Scan

Scan Left (Prefix sum problem)

xs.scan left(x)(f) 接受一個initial value x，回傳一個新的list ys( x, y1=f(x, xs[0]), y2=f(y1,xs[1]), f(y2,xs[2]), ... )

假設f 是associative。

sequential版本如下:

parallel版本:
首先output array中的每個element其實都有獨立的計算可能，不需要真的依賴前一個element被算完才能計算，所以parallelism是可以實現的，例如:

out(0) = a0
out(1) = a0+inp(0)
out(2) = a0+inp(0)+input(1)
.
.
.

這個的問題在於每個out(i)都重覆計算了out(i-1)的動作，這是parallelization的overhead，但是parallism的效益會補償這個損失。

假設我們要用之前提過的parallel版本的array segment reduce和 array segment map來implement parallel scan的話，該怎麼做呢?

注意mapSeg中的fi接受index參數和input array value參數。

這邊有點複雜:

首先mapSeg把input array parallel的分成一半，再一半，一直下去，直到不能分(array size <threshold)之後，就apply sequential map function，此時fi 就會被呼叫在那一段base case的array上，注意fi 接受參數(array position index, pointer to array position)。

所以reduceSeg1就會作用在array區間0 ~ i (exclusive)的array上，把0~i都根據f和initial value a0 reduce成某一個數值。這邊應該要叫做fold才對吧，fold才有initial value，reduce是沒有的，實在很混淆。

output由於比input array多一個element，所以我們無法透過mapSeg得到output的最後一個element，必須要在最後兩行手動算出output的最後一個element。

以上的版本是獨立算出output所有的element，完全沒有使用已算好的intermediate values。

重複利用intermediate results when reduce

parallel版本有辦法使用到中間算到的結果嗎?
首先注意reduceSeg1是使用tree structure做reduction，這邊先假設reduceSeg1 input collection也是tree data structure:

不過由於我們想要儲存已經算過的value，我們改寫以上tree定義如下:

可以看到在有一個res field。

相對應的sequential reduce function:

以下是一個執行範例:

首先我們create tree t1，以及定義binary operation plus
接著執行reduceRes(t1, plus)
結果回傳了一個tree，每個node都有一個value，non-leaf node的value就是左右children res的binary operation的結果。

而root其實就是整個collection的reduce結果。(廢話)


parallel版本: 稱為upsweep (因為這等於是從leaf往上得到root reduction結果)

可以看到也是parallelize tree traversal ( task splitting)

那怎麼使用在scanLeft? 這邊又要假設scanLeft是要接受一個tree collection，總之這邊的input / output collection都是以tree的狀態存在。

所以scanLeft的input collection是一個upsweep過後的tree，所有的nodes res values都填好了，包括root 在內，這時候t又有一個新明子，稱為downsweep， 因為我們要從tree往下得到scan left的new collection:

這老師解釋實在很爛，看code比較快!
downseep從root開始會parallel往leave跑，直到leaf之後，就要產生新的collection 該有的leaf值，但是注意對左邊的child來說，value = f(a0, leaf.res)，但是對右邊的child來說，value = f(f(a0, sibling.res), leaf.res)，這其實就是scanLeft的定義: new collection中的某個數字，是前面subtree reduction後的結果+initial value

假設parallelism由左至右跑的情況: (a0 = 100, f = +)
leaf(1) 得到 f(100, 1) = 101
leaf(3) = f(f(100,1),3) = 101+3 = 104
leaf(8) = f(f(100,4),8) = 104+8 = 112
leaf(50) = f(f(f(100,4),8), 50) = 112+50 = 162

每個node (non-leaf)的a0如下:

不過注意downsweep不會包括a0!

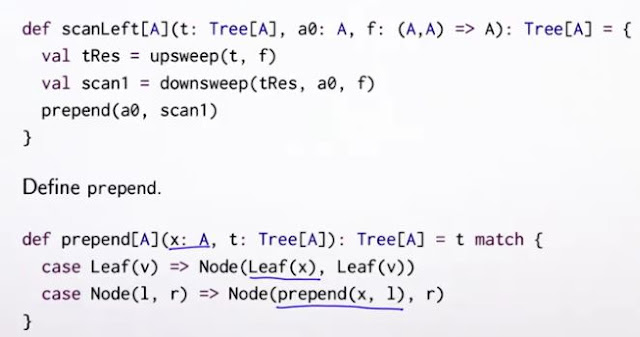
最後可以寫出完整的scanLeft，當然也是採用tree input / output:

如果input是一個array，而非tree呢? 我們仍然用一個tree來儲存intermediate values，leaf不是單一數值，而是某個array segment:

upsweep:

reduceSeg1 (Sequential):

downsweep:

scanLeftSeg (sequential):

scanlefg:

附註: Scan Right

scanRight結果跟scanLeft很明顯會不同，因為initial value被插在list最後面: