Scala Parallel Programming筆記 11 - Splitter and Combiners

Iterator 

首現我們知道Java有iterator:

Splitter (iterator parallel counterpart)

每一個parallel collection都依定會implement Splitter trait。
一但呼叫了split，就分成幾個disjoint splitter set:

原來的splitter instance會變成undefined state。
remaining是"estimate"目前splitter中有幾個element。

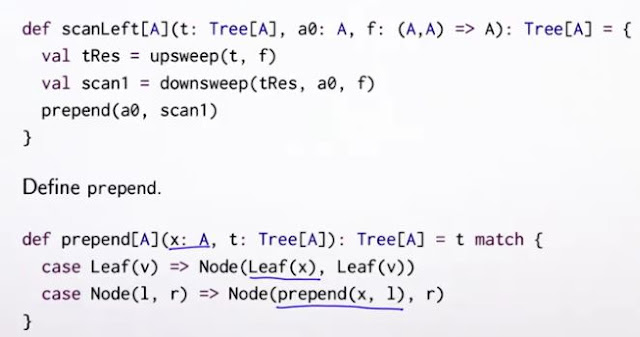
來看怎麼用splitter trait implement fold?

首先迴響 for .. yield會產生一個collection，所以children是一個collection for task[Splitter]，每個task會recursively呼叫fold，由於每次children都是remaining > threshold時 split出child Splitters而來，所以remaining會越來越少，直到抵達base case去做sequential foldLeft。最後一行還是要記得去呼叫foldLeft在這個children collection上，才能真正去merge。

Builder

result被呼叫的話，就會return collection，而此builder就undefined。

所以builder其實是把一個collection的“增加member"這件事抽象化的trait，

Combiner (parallel Builder)

combiner要efficient需要經過一番努力，所謂的efficient是要在O(logn + logm)時間內完成，當然落，要不然不等於linearly跑過一次，那哪叫什麼efficient combiner。簡單以四核心cpu為例：

一個reduction tree的leaves會分配給4 core cpus，假設剛好分成四份，每份1/4 N，但是在往root combine的過程中，其實總共累積了（粗略計算） 7/4 N > N的工作量，這比單一cpu sequentially map的時間還久！！！

combine對Map/Set來說，是union。
對sequence來說 (List/Vector/Array) combine是concatenation。

可惜的是，對常見的data  structure來說，combine的動作不可能達到efficient (O(logm + logn)。

兩階段parallel construction

但是實際上幾乎所有的scala collection都能轉換成parallel collection，為何？
因為採取了兩階段的collection construction，使用暫時的data structure來儲存state，例如Array 可能採用其他的intermediate data structure來表現，使得efficient combiner可以實現。

這個intermediate data structure有以下的性質：

第三點就是builder/combiner為什麼會有result method的原因，因為要捨棄這個intermediate data structure，convert到真正的data structure，需要再O(n/P) time內，n = size of the data structure, P = # processors。這個convert必須也要能parallellizable。

phase 1：每個processor先呼叫 += 來build intermediate data structures，然後每個ids被combine直到reduction tree root。

phase 2: parallelly build final data structure from ids。

總共約N/2 for 4 processors。

Array Combiners

intermediate data structure主要就是nested array:

先來看怎麼implement += :

這是O(1)。如果裏層array滿了，就new一個新的更大的。注意上圖中其他的第一層array element都是空的。

combine就很簡單了，因為第一層array是一堆Array pointer，所以只要指向另一個被combine的nested array就可：

這邊 ++= 倒是第一次看到的operator! 這是constant time operation 。

再來是conversion result:

後來的筆記都消失了....因為chrome給我當機 @@
火大ㄟ

Scala Parallel Programming筆記 10 - Scala parallel collections

Sequential Collection Hierarchy

Parallel Collection Hierarchy

注意中間的generic collection系列是用在當collection未知是sequential or parallel的時候。

舉例來說，如果要找某個array中最大的palindrome:

由於xs是一個GenSeq[Int]，所以只要是這個trait的subclass都能不管是否真的parallel或是sequential而去呼叫以下：

.par conversion time

把一個collection轉換成parallel collection是需要時間的，一個100萬element的list需要128 ms，而一個100萬elements的vector只需要0.0015 ms，這是由於list並非parallelizable collection，所以scala把list轉換成最接近形式的parallel collection: vector。

以下是parallel collections:

所以挑選一個parallel collection要很注意！不要選錯。

小心使用thread-unsafe collection

以下是一個錯誤的範例：

這邊有個讓我發現我觀念錯誤的地方就是，其實不是把0 until 1000給拆成總共加起來是1000個的數份collection，而是語意會達成sequential的語意，也就是應該會拆成{parallel set a} x {parallel set b} 的組合（但是這樣應該會重複計算？ 不過parallelism會彌補），要不然帶入setA和setB都是disjoint parallel set的話，就變成{parallel set a} x {parallel set b} 組合的其中幾種，而且結果會是不確定的。所以不是我想的那樣，但是這個寫法還是錯！

錯誤在於mutable.Set是not thread-safe，所以每次+=都會update同一個object（同時也驗證上面講的{parallel set a} x {parallel set b} ），所以會錯。

其中一種解決方法是改用thread-safe collection取代mutable.Set:

另一個方法是使用combinator，避免mutation side effects:

這邊所謂的combinator是指"filter" ，丟入b(_)，課堂中講這是似乎有Int=>Boolean的signature，所以是一個function object，代表把set b整個丟入去filter。
其實光是a.filter(b(_))即可，但是如果要efficient，就可以用比較小的set去當filter parameter。

不要在mutable collection traverse時 update / read

這個就算在sequential case也成立。
請看以下錯誤範例：

這邊錯誤(1)在traverse graph.par時，graph(k)被寫入graph(v)，我們不能在traverse的過程中還update。(2) graph(v) 這是一個read operation，但是collection卻正在被(1) update！因為mutable.Map不是一個thread-safe collection!!!!

TrieMap collection

上面的問題可以用一個concurrent TrieMap collection來解決：因為TrieMap提供了atomic snapshot功能，能把某個state確切snapshot起來（在collection.par開始時），所以之後的traverse都是用這個snapshot，而之後的update都不會被看見。

所以這邊有三個graph instance:
1. 在graph.par (被convert成parallel collection)時，一個紅色的snapshot被“隱性自動的”建立了，此snapshot在traverse過程中都一直被用到，所以graph(k) = previous(v)不會影響此紅色snapshot

2. 藍色的instance就是這個TrieMap本身，是mutable，真正的update在這個collection

3. 粉容色的instance是一個我們自己建立的snapshot，這是用來保存update之前的狀態，因為此program有需要用到。

這樣有了1，我們就不會在traverse時候遇到內容被update會打亂traverse state的問題
有了3，我們就不會遇到去讀正在update的graph裡面的某個value，可能state被打亂的問題。

Scala Parallel Programming筆記 9 - Data Parallel Operations

fold construct

scala collection多數能直接轉成parallel collection，透過.par method:

所以filter / count 都可以execute in parallel。例如我們可以寫一個collection sum:

def sum(xs:Array[Int]):Int = {
  xs.par.foldLeft(0)((x,y) => x+y)
}

可惜foldLeft不能直接parallelize，先看其signature:

所以foldLeft accumulator type B，collection element type A，透過f(B,A) => B來把每一個element fold成一個單一值。但是每次進入f的B其實是前一次f的output，也就是foldLeft只能sequential computation。

fold/reduce/scan 都是只能sequential operation。

如果fold是以下的signature的話，就可以用parallelization (reduction tree):

事實上scala有fold function，是專門給parallel computation用的。當然要用parallel fold還是得要遵守operator必須是associative的前提，舉例來說，以下的operator (play剪刀石頭布)只有communtative，但是不associative，所以不同的execution order會有不同的結果：

所以初始值(z)和binary operator f必須滿足以下性質（稱為monoid關係）：

所以z丟進去f其實就是a的identity function。

可是fold很明顯不夠用，因為所有參數都只能是same type，這只能用在受限的application context。

Aggregation construct

解決fold不夠expressive的問題，另一個parallel operation稱為aggregation:

比較特別的是，他接受兩個operators f and g，f是sequential operator, g是parallel operator，為什麼要這樣？

注意f是跟foldLeft的operator f一樣的signature，而g的signature是跟fold的operator一樣的signature，所以aggregation事實上是combine foldLeft 和 fold:

所以把array 先分成不同parts，然後每個parts用sequential foldLeft，最後用fold combine，不過問題是，為什麼這樣可以？

舉以下的例子：

的確這是可行的，因為sequential的f不依賴任何其他parts results，而parallel的g符合monoid structure ( 0 + count = count 且 + operator是associative )。

Scala Parallel Programming筆記 8 - Data Parallelism

Task parallelism vs Data parallelism

之前講的都是task parallelism，也就是怎麼把一個program，分成好幾個平行處理的tasks。現在要講的是，怎麼把data變成可以丟給不同processor平行處理的data? 因為data進來的狀況不見得適合平行處理。

一個可能的data parallelization是parallel for:

上面這個function把v寫到xs所有elements中。
把(0 until xs.length)這range呼叫par方法，就能把壹些range分散給不同processor，但是這個方法是把v寫入xs，這是side effect，not pure functional (not input -> output)，因為使用到了side effect，這有賴於parallel range不會重疊，否則就有race condition的問題。

Mandelbrot set example

假設c為複數平面任一點，定義mandelbrot set如下，這個值如果絕對值 < 2，就屬於mandelbrot set:

如果把複數平面畫成一個image，如果把不收斂（many iterations之後，和的絕對值 >= 2，也就是)的iteration數目mapping到顏色的話，長這樣：

所以收斂的pixel我們不填值，是黑色的，不是黑色的pixel都是發散的pixel。以下是sequential mapping 發散pixel顏色的方法：

如果要data parallelization的話：

如果用task parallelization (reduction tree)，速度是最慢的。如果用data parallelization (scala parallel collection)，速度比task parallelization約快25%。如果用data parallelization + workload balancing scheduler，速度會達到task parallelization的兩倍！

由於mandelbrot set中的pixel值的workload是跟他的iteration數目成正比，而不是const cost，所以藉由workload balancing機智，能夠比task parallelization快上兩倍。

Scala Parallel Programming筆記 7 - Prefix sum作業2

Counting change problem in parallel

這個問題的sequential版本在此，又忘記了，哈哈。
這題目還不錯，把n=4和denomination =[1,2]的tree都畫出來，這樣很好理解：

填入countChange的sequential版本，問題是怎麼parallelize?

首先要決定thresholding for agglomeration，agglomeration就是避免parallelism的recursive depth太深，這其實有可能造成很大的synchronization overhead (multithreading是有synchronization overhead)，所以到當input size < threshold （base case)，我們就該停止recursion，然後採用sequential processing。

要寫出parallel版本的countChange不難，就仿照lecture中的簡單範例就可以，但是問題在於threshold怎麼設計？

“Counting change is a canonical example of a task-parallel problem in which the partitioning the workload across processors is solution-driven -- to know how to optimally partition the work, we would first need to solve the problem itself.”

這作業的目的就是要我們知道，即便可以做task parallelization，怎麼分配task load是一個問題，而且需要先解出這個母問題才能解出task load怎麼分配的問題，雞生蛋蛋生雞的問題。這邊難處在於我們不能判斷sequential版本要花費多少時間，不像是array segment那樣容易推理。

作業採用了3種thresholding heuristics，要我們試驗看看哪個比較好？
speedup ~= 3.x倍

Balancing Parentheses in Parallel

這題其實很簡單，但是traverse function的提示誤導了人，多了那兩個int 其實是給recursion用的，如果寫while的話，就完全用不到這兩個ints。

這題目的sequential版本很直接的簡單，但是parallel版本就有點需要思考，首先要知道每次reduce的時候(想像成recursion tree中的non-lead node)，兩個children其實一定是consecutive array segments，所以真正要消除配對的括號要在此階段做，-而不能在sequential traverse中做。

關鍵點在reduction operator其實是找出兩個consecutive segment抵銷matching bracket之後的左右brackets數量。

def parBalance(chars: Array[Char], threshold: Int): Boolean = {

  def traverse(idx: Int, until: Int, arg1: Int, arg2: Int) :(Int,Int)  = { //returns (#left brackets, #right brackets) if not cancelled    var i = idx
    var leftBracketCount = 0    var rightBracketCount = 0
    while (i < until) {
      if (chars(i) == '(') {
        leftBracketCount += 1      }
      else if (chars(i) == ')') {
        if (leftBracketCount != 0)
          leftBracketCount -= 1        else          rightBracketCount += 1      }

      i += 1    }
    (leftBracketCount, rightBracketCount)
  }

  def reduce(from: Int, until: Int) : (Int, Int) = {
    if (until - from <= threshold)
      traverse(from, until, 0, 0)
    else {
      val mid = (from + until)/2      val ( (aLeft:Int,aRight:Int), (bLeft:Int,bRight:Int) ) = parallel(reduce(from, mid), reduce(mid, until))

      val leftCount =
        if (aLeft >= bRight ) aLeft - bRight + bLeft
        else bLeft

      val rightCount =
        if (aLeft >= bRight ) aRight
        else aRight + bRight - aLeft

      (leftCount, rightCount)
    }
  }

  reduce(0, chars.length) == (0,0)
}

Line of sight in Parallel

題意要先搞清楚。一個x軸為水平位置，y軸為高度的terrain:

要計算每個x位置的visibility，但是規定視線只能往上，不能往下，也就是如果tan(x1) > tan(x2)，則visibility(x2) = visibility(x1) = tan(x1)，反之visibility(x2) = tan(x2)，所以sequential 版本的 line of sight很簡單如下:

def max(a: Float, b: Float): Float = if (a > b) a else b

def lineOfSight(input: Array[Float], output: Array[Float]): Unit = {
  var i = 1  output(0) = 0
  while(i < input.length) {
    val tangent = input(i) / i
    output(i) = max(tangent,output(i-1))
    i += 1  }
}

我們要怎麼改成parallel版本?
這是一個prefix sum problem，也就是output(n+1) = f( output(n), input(n+1)，a0 = 0 ，因為一開始在原點沒有位移，所以斜率=0。

我們要先建立reduction tree，透過upsweep 過程。
reduction tree的用意其實就是一個可以parallelize的tree structure，此reduction tree會在每個node都儲存apply f這樣才能進行downsweep。

一個upsweep的reduction tree應該是長這樣:

                              max
                          |            |
                        max       max
                     |          |     |      |
                  [   ]     [   ]  [  ]  [  ]

注意leaf不一定是single value(因為會有threshold來控制parallel depth)，如果是一個array或是collection，則就相當於找出以此為root node的subtree的reduction value，但是在downsweep的時候又要sequential跑一次。

所以基本上這就是模仿課堂中的prefix sum範例就好。
這門課的作業test case給得很少，可以submit時放入log來debug。

Scala Parallel Programming筆記 6 - Parallel Scan

Scan Left (Prefix sum problem)

xs.scan left(x)(f) 接受一個initial value x，回傳一個新的list ys( x, y1=f(x, xs[0]), y2=f(y1,xs[1]), f(y2,xs[2]), ... )

假設f 是associative。

sequential版本如下:

parallel版本:
首先output array中的每個element其實都有獨立的計算可能，不需要真的依賴前一個element被算完才能計算，所以parallelism是可以實現的，例如:

out(0) = a0
out(1) = a0+inp(0)
out(2) = a0+inp(0)+input(1)
.
.
.

這個的問題在於每個out(i)都重覆計算了out(i-1)的動作，這是parallelization的overhead，但是parallism的效益會補償這個損失。

假設我們要用之前提過的parallel版本的array segment reduce和 array segment map來implement parallel scan的話，該怎麼做呢?

注意mapSeg中的fi接受index參數和input array value參數。

這邊有點複雜:

首先mapSeg把input array parallel的分成一半，再一半，一直下去，直到不能分(array size <threshold)之後，就apply sequential map function，此時fi 就會被呼叫在那一段base case的array上，注意fi 接受參數(array position index, pointer to array position)。

所以reduceSeg1就會作用在array區間0 ~ i (exclusive)的array上，把0~i都根據f和initial value a0 reduce成某一個數值。這邊應該要叫做fold才對吧，fold才有initial value，reduce是沒有的，實在很混淆。

output由於比input array多一個element，所以我們無法透過mapSeg得到output的最後一個element，必須要在最後兩行手動算出output的最後一個element。

以上的版本是獨立算出output所有的element，完全沒有使用已算好的intermediate values。

重複利用intermediate results when reduce

parallel版本有辦法使用到中間算到的結果嗎?
首先注意reduceSeg1是使用tree structure做reduction，這邊先假設reduceSeg1 input collection也是tree data structure:

不過由於我們想要儲存已經算過的value，我們改寫以上tree定義如下:

可以看到在有一個res field。

相對應的sequential reduce function:

以下是一個執行範例:

首先我們create tree t1，以及定義binary operation plus
接著執行reduceRes(t1, plus)
結果回傳了一個tree，每個node都有一個value，non-leaf node的value就是左右children res的binary operation的結果。

而root其實就是整個collection的reduce結果。(廢話)


parallel版本: 稱為upsweep (因為這等於是從leaf往上得到root reduction結果)

可以看到也是parallelize tree traversal ( task splitting)

那怎麼使用在scanLeft? 這邊又要假設scanLeft是要接受一個tree collection，總之這邊的input / output collection都是以tree的狀態存在。

所以scanLeft的input collection是一個upsweep過後的tree，所有的nodes res values都填好了，包括root 在內，這時候t又有一個新明子，稱為downsweep， 因為我們要從tree往下得到scan left的new collection:

這老師解釋實在很爛，看code比較快!
downseep從root開始會parallel往leave跑，直到leaf之後，就要產生新的collection 該有的leaf值，但是注意對左邊的child來說，value = f(a0, leaf.res)，但是對右邊的child來說，value = f(f(a0, sibling.res), leaf.res)，這其實就是scanLeft的定義: new collection中的某個數字，是前面subtree reduction後的結果+initial value

假設parallelism由左至右跑的情況: (a0 = 100, f = +)
leaf(1) 得到 f(100, 1) = 101
leaf(3) = f(f(100,1),3) = 101+3 = 104
leaf(8) = f(f(100,4),8) = 104+8 = 112
leaf(50) = f(f(f(100,4),8), 50) = 112+50 = 162

每個node (non-leaf)的a0如下:

不過注意downsweep不會包括a0!

最後可以寫出完整的scanLeft，當然也是採用tree input / output:

如果input是一個array，而非tree呢? 我們仍然用一個tree來儲存intermediate values，leaf不是單一數值，而是某個array segment:

upsweep:

reduceSeg1 (Sequential):

downsweep:

scanLeftSeg (sequential):

scanlefg:

附註: Scan Right

scanRight結果跟scanLeft很明顯會不同，因為initial value被插在list最後面: