Sonny不讀不行: 了解gradient descent背後的數學

了解gradient descent背後的數學

machine learning中常用到的gradient descent是多變數微分的應用，這篇筆記算是把背後的數學意義記錄下來。前面幾段是基礎知識，如果已經懂了，可以直接跳到後面directional derivative去看。

R^3是一個set，包含R^3的定義

R^3是一個set，包含所有不同順序的ordered 3-tuple的點：

cross product (vector product) of 2 vectors

定義如下：

這是在找出同時垂直於兩個vectors形成的平面的向量，所以還是另一個向量！

determinant （這只是一個運算元）

order 2定義：

order 3定義：

general定義就是 ai * （去掉自己row和col的所有數字的縮小版determinant)

我們可以把3-d vector cross product用determinant重寫：

或者寫成同一個determinant，但此時ai變成vectors，所以算出來的determinants也是vectors:

2-variable function

z=f(x,y)，畫圖在R^3可能長這樣：

如果x和y都是一次的，也沒有相乘，則是一個linear function，在R^3中會是一個平面：

例如： f(x,y) = 6 - 3x - 2y

例如: z = 4x^2 + y^2。橫切面是橢圓形 (ellipses)，縱切面是拋物線(parabolas)。

另外幾個例子

等高線圖 (level curve / contour)

這個其實就是z的多個橫切面投影在xy平面上的圖，常見的有等高線圖之類的。

Derivative

先說定義：

如果以single variable function來說的話，f'(a) 是f(x)在x=a的地方的切線的斜率：

物理上的意義是“改變的速率” (rate of change)。
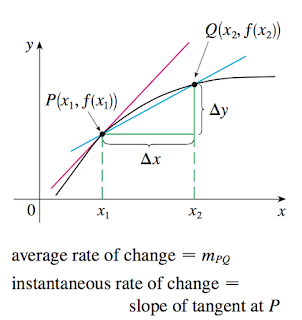
假設某y = f(x)，所以當x改變的量為delta x = x2 - x1，y改變的量即為 f(x2) - f(x1)，所以改變的幅度：

這稱為y對x的平均改變速度 (average rate of change of y with respect to x)。這是一個平均的概念。

如果delta x趨近於零，也就是當x改變了能夠想像的最小程度，則上式就是“瞬間” instantaneous rate of change with respect to x1

也就是所謂的 derivative f'(x1)

看圖可以理解這就是在x1的切線斜率：

距離公式s(t)，瞬間速度是s'(t) ＝距離這個變量的“rate of change" ，對時間這個變量來說。（白話文：時間t的改變造成距離s改變的程度）。

derivatives of two-variable function

假設有一個function z = f(x,y)在R^3中是一個曲面s:

如果我們固定y = b，則相當於形成一個function z = f(x,b)，這就是上圖中S的縱切面形成的曲線C1。同理如果固定x = a，會形成曲線方程式 z = f(a, y) = C2

這兩條曲線各自有自己的在P點的切線T1和T2，其斜率為z在P點的導數。
對C1來說，在P點的切線T1的斜率意味著 x=a且y=b的時候，x的改變造成z的改變的rate of change。

同理對C2來說，則是x = a且y = b的時候，y的改變造成z的改變的rate of change。

我們定義partial derivatives functions為：

有很多種表達法 @@

所以T1, T2的斜率就是fx(a,b) 和 fy(a,b)。

general case: directional derivative

解讀partial derivatives的意義：

這是一個等溫線圖，溫度I = f(lat,lon)。所以f_lat ＠ Reno的意思就是從Reno出發的話，溫度相對於緯度（距離）的變化速度（rate of change)，f_long也是類似的意思。

但是看等溫線圖可以發現溫度呈現越東南越高的狀況，也就是任一方向的溫度相對於距離的rate of change有可能是正負值。

假設此f在3d空間中形成一個surface S:

如果我們任意選擇一個方向（向量u)，對S立下一個垂直切面，則此切面會與S交會在curve C。此C上的u方向上的交點P(x0,y0,z0)，其切線為T。要怎麼找到此T的切線斜率？

另取C上另一點Q使得PQ組成一向量，則此向量PQ在xy平面的投影向量為h*u，則PQ的斜率可以用：

對PQ斜率取極限值就是T的切線斜率，這就是derivative的定義，但是在這邊是f在u方向上的derivative:

所以f_x和f_y其實只是某兩個特例的directional derivative，剛好在standard basis vector i和j的方向而已。

上圖其實也暗示了directional derivative其實可以拆成i和j方向的兩個分量，意思是所有的directional derivative都可以用f_x和f_y表示：

Gradient vector function

theorem 3可以寫成dot product形式：

u前面這個vector function，有一個特殊名稱，叫做"gradient" of f：

所以gradient是所有standard basis vector方向上的partial derivative合成的vector function。

所以反過來看，也可以說directional vector是gradient在u方向上的投影：

延伸到多變數：

舉例來說：

按照directional derivative和gradient的關係，可以先找出f的gradient vector function:

再來算出f在(2,-1)時的gradient vector:

再來就可以算出directional derivative，這就是gradient在u方向上的投影，但是題目中的v不是unit vector，所以還要將之轉換成unit vector，算出來的答案才會正確：

如何找出最大的directional derivative?

在machine learning中常常用到的optimization方法之一就是gradient descent，為了要快速收斂找到model f的minimum cost，我們需要在f形成的surface S上，從某一個初始點找到切線斜率（directional derivative, rate of change of f respect to 某個feature)最大（最陡）的方向去下降（descent)，所以如何找出最大的directional derivative是我們好奇的。

這很簡單可以找出來：所有方向中的derivative只有與gradient的方向一致 (夾角為零）時，rate of change最大：